算法学习 - 二叉 B-树 (Binary B-Tree) 与对称二叉 B-树 (Symmetric Binary B-tree)

October 14, 2024

最近准备好好学习一下 红黑树, 但在过程中感觉到其中很多操作和变换都比较 “魔法”, 简而言之就是难以直接理解为什么要这样操作. 现在网络上主流的两种理解方式为: “算法导论” 中的双黑法与 2-3-4 树等价的思路. 不过这些文章还是不没让我明白 红黑树 为什么要这么设计, 操作之间的内在逻辑是什么. 因此这篇文章想从另一个角度聊探究一下红黑树的 “历史”.

以下内容一些来自论文原文或翻译, 一些来自互联网上的其他文章, 还有一些为自己的理解, 如有错误还望能够在评论中指出.

B-树 (B-Tree)

B-Tree, 1970 年由 Bayer,R 与 McCreight,E 于 “ORGANIZATION AND MAINTENANCE OF LARG” 中首次提出. B-Tree 在处理大规模数据时提供高效的搜索, 插入, 删除和范围查询操作, 即使在现在也作为各大数据库的底层存储数据结构. 这里简单复述一下 B-Tree 的定义和性质:

节点定义, B-Tree 有两种节点:
- 内部节点 (INTERNAL): 存储 Key 及其指向子树的指针.
- 叶子节点 (LEAF): 只存储 Key.
性质, 对于一个 m 阶 B-Tree, 将满足:
1. 每个节点最多拥有 m 个子节点
2. 除 ROOT 和 LEAF 外, 每个节点最少看拥有 cell(m/2) 个子节点.
3. ROOT 节点除非是 LEAF, 否则子节点数 >=2.
4. 有 k 个子节点的节点拥有 k-1 个 Key, 按照升序 (asc) 排序, 即满足 k[i]<=k[i+1]
5. 所有叶子结点都在同一层.

不过这次不深入讨论它, 只是为了引出下面的数据结构.

二叉 B-树 (Binary B-Tree)

Binary B-Tree 由 Bayer,R 于 1971 年 “BINARY B-TREES FOR VIRTUAL MEMORY” 中提出. 正如该论文的摘要中所属, 该结构是为了解决 B-Tree 遇到的存储开销, 使其更适合在单极存储 (one-level store) 中进行处理.

Binary B-trees are a modification of B-trees described previously by Bayer and McCreight. They avoid the storage overhead encountered with B-trees and are suitable for processing in a one-level store.

不严谨的概述: 更适合在 “内存 (或虚拟内存)” 而不是 “内存-硬盘” 这类多级存储中使用的数据结构.

假设一个 k=1 的 B-Tree, 则节点可能存在以下两种方式:

| p0 x1 p1 - - |      | p0 x1 p1 x2 p2 |

    x1 | -               x1 | x2
  /    |       or       /   |   \
p0     p1              p0  p1   p2

可以看到, 根据上一节提到了性质 2, 每个节点可能是 “半满” 的, 这在内存中会造成浪费. 并且每个 B-Tree 节点在创建时都需要为其分配存储空间, 这在那个内存寸土寸金的年代也是不可接受的.

二叉 B-树提出了一种可能的优化方法: 使用 “线性链表” 而不是数组存储. 因此上面的结构变为如下:

| p0 x1 p1 - - |      | p0 x1 p1 x2 p2 |

    x1                   x1 ->  x2
  /   \        or       /     /   \
p0     p1              p0    p1   p2

论文中将 x1 指向 x2 的指针称为 “水平的 (horizontal)” (σ-pointer), 而指向 “下一级” (子节点) 的指针称为 “垂直的 (vertical)” (δ-pointer).

转化后的如图所示 (Binary B-Tree 很像 AVL, 但是不是 AVL):

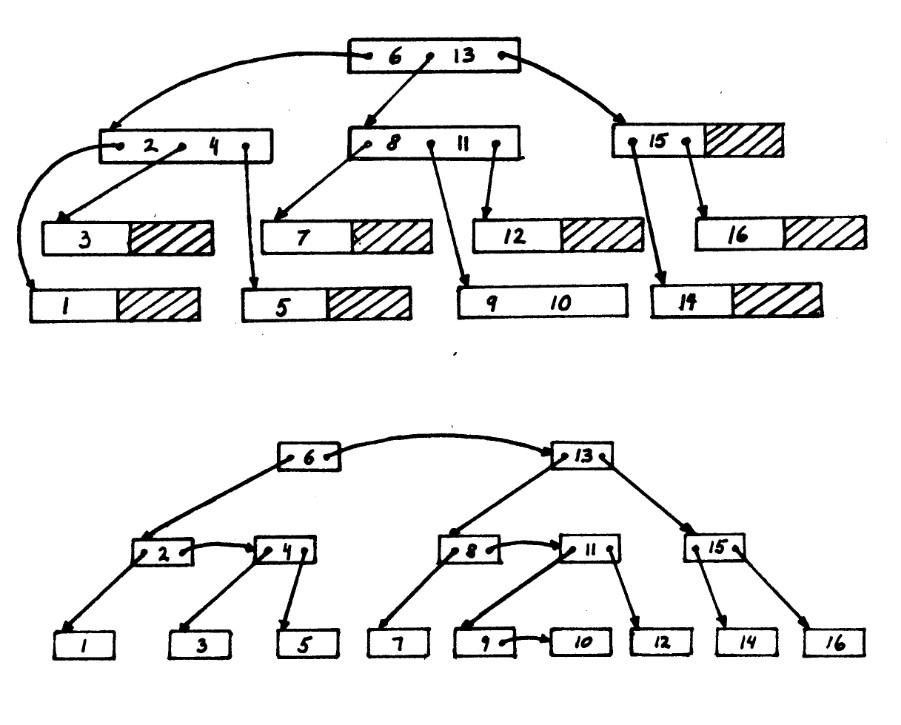
Binary B-Tree

下面引出相关定义:

节点分为以下两种:
- NODE: 普通节点, 具有至少一个 δ-pointer.
- LEAF: 叶子节点, 没有 δ-pointer.

// NODE
      x1            x1 -> x2
     /   \          /    /  \
    p0    p1       p0    p1   p2

// LEAF
    |       |             |
    x1     [x1] -> x2     x1 -> [x2]

所有左指针都是 δ-pointer.
从 ROOT 到任何叶子节点的每条路径都包含相同数量的 δ-pointer.
一些右指针可能是 σ-pointer, 但不存在连续的 σ-pointer. 即每一个 σ-pointer 指向节点的只能为 LEAF 或者右指针为 δ-pointer.

一颗 N 个节点的二叉 B-树的高度为 (计算方法见论文第 222~223 页):

log(N+l) <= h i <= 2log(N+2)-2

从上面高度范围可以看出, 二叉 B-树并不是一个 “很平衡” 的树. 下面给出插入和删除的操作概要:

二叉 B-树插入 (Insert)

将新节点 x 插入叶子节点时, 存在以下情况:

LEAF 是孤立的 (case1).
LEAF 所在层的路径上存在 σ-pointer (case2).

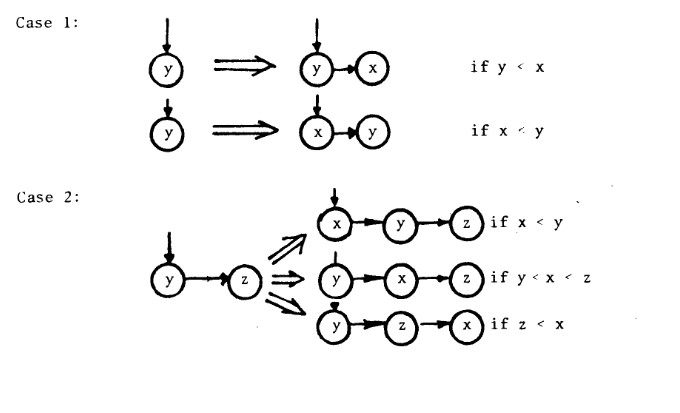
Binary B-Tree Insertion

针对 case1, 直接插入到 σ-pointer, 算法结束.

针对 case2, 因为违反了 性质3 (引入了两个 σ-pointer), 因此需要通过 TRANSFER 过程将其移除. 这是一个递归的过程, 直到没有连续的 σ-pointer 或者到达 ROOT 节点.

// Right, 如果 x0 缺失, 则 x4 成为新的 root.
x0                           x0 - x4        // 提升了一层, 但是这里可能又出现类似 x-x0-x4,
 \                              /   \       // 需要递归处理.
  x2 - x4 - x5   -->          x2     x5
 /    /                      /  \
x1  x3                      x1   x3

// 等价
    x0                           x0 | x4
      \                        /    |   \
  x2 | x4 | x5   -->        ...    x2   x5
 /   |                           /   \
x1   x3                        x1    x3

// Left, 如果 x5 缺失, 则 x3 成为新的 root.
     x5                      x3 - x5
    /                       /    /  \
   x1 - x3 - x4  -->      x1    x4   ...
  /    /                 /  \
x0    x2                x0  x2

// 等价
        x5                  x3 | x5
       /                  /    |   \
  x1 | x3 | x4   -->    x1    x4    ....
 /     |              /   \
x0     x2            x0    x2

二叉 B-树删除 (Deletion)

先找到要删除的 Key 所在节点 z, 这里分为两种情况:

Key 所在节点为 LEAF
Key 所在节点为 NODE

针对第二种情况, 我们需要转变为第一种情况, 寻找 Key 所在节点中序遍历的后继结点 y (successor), 将 y 节点的值替换 z 节点的值, 然后准备删除 y (此时已经回到了情况 1).

将需要删除的节点替换为一个哑节点 d (Dummy), 完成第一步.

// case1
|          |           |
z[d]       z[d] - x    x - z[d]

// case2
|              |
z              y
 \              \
  ...   -->      ...
  /             /
 y             y[d]  // 此时回到 case1

删除节点后, 可能违反 性质2, 因此需要向上修复性质. 需要先明确, 删除后只有一种情况需要修复:

|
z[d]

而其他两种情况可以直接删除 d 即可.

我们先考察初始情况, 此时考察 d 节点的兄弟节点 (一定存在). 如果兄弟节点存在 “多余的节点” (存在 σ-pointer 指针), 则从兄弟节点 “借” (ADOPT) 一个节点过来, 完成修复; 否则将节点, 兄弟节点与父节点 “合并” (MERGE), 将 d 节指向向上推一层:

d 位于右侧 δ-pointer 时, 必定存在兄弟节点, 此时存在两种情况 case 1a 与 case 1b 如下:

// case 1a: d 位于右侧 δ-pointer 且兄弟节点 x1 没有多余的节点可以借用
     \                      \
      x3                     d
    /   \                    |
  x1     d    -- MERGE -->   x1 - x3      --> ...
 /  \    |                  /    /  \
x0  x2   x4                x0   x2   x4

// case 1b: d 位于右侧 δ-pointer 且兄弟节点 x1 可以借用多余的节点
       \                                \
        x5                               x3
    /        \                         /    \
  x1 - x3     d    -- ADOPT -->     x1        x5      (DONE)
 /    /  \    |                    /  \      /  \
x0   x2   x4  x6                  x0   x2   x4   x6

d 位于左侧 δ-pointer 时, 兄弟节点可能存在于同一个父节点或者父节点 σ-pointer 所在节点的左子树上, 此时存在 4 种不同的情况, 分为:

兄弟节点位于同一个父节点: case 2a, case 2b
兄弟节点在另一个节点上: case 3a case 3b

// case 2a: d 位于左侧 δ-pointer 且兄弟节点 x2 没有多余的节点可以借用
    \                         \
    x1                         d
  /   \                        |
  d   x2    -- MERGE -->      x1 - x2
  |                          /
  x0                        x0

// case 2b: d 位于左侧 δ-pointer 且兄弟节点 x3 可以借用多余的节点
    \                               \
    x1                              x3
  /    \                           /   \
 d      x3 - x4   -- ADOPT -->    x1   x4         (DONE)
 |     /                         /  \
 x0   x2                        x0  x2

// case 3a: d 位于左侧 δ-pointer, 兄弟节点 x3 位于父节点 σ-pointer 指向节点, 兄弟节点存在 σ-pointer
  \                                   \
   x1 -  x5                            x3 -  x5
  /     /                             /     /
 d     x3 - x4   -- ADOPT -->       x1    x4      (DONE)
 |    /                            /  \
 x0  x2                           x0   x2

// case 3b: d 位于左侧 δ-pointer, 兄弟节点 x2 位于父节点 σ-pointer 指向节点, 兄弟节点孤立
  \                                   \
   x1 -  x3                            x3
  /     /                           /
 d     x2        -- ADOPT -->      x1 - x2        (DONE)
 |                                /
 x0                              x0

现在看会 case 1a 与 case 1b, 可以发现合并 (MERGE) 后可能会产生一种新的情况, 以 case 1a 为例:

// case 1a
   (\) (/)                  (\) (/)
  (-) x3                   (-) d
    /   \    -- MERGE -->      |
  x1     d                    x1 - x3
 /  \

此时如果为 - d, 则不满足上述的任何情况, 因此引入 case 4:

// case 4
  \                  \
  x1 - d    -->      x1       (DONE)
 /     |            /  \
x0    x2           x0   x2

二叉 B-树算法时间

通过上述操作, 我们可以得出, 二叉 b-树 的随机查询, 插入和删除时最坏的情况下与树的高度成比例, 即 Θ(lgN)，其中 N 是树中 Key 的数量.

二叉 B-树小结

其实我们已经能从 二叉 B-树 中看到一些红黑树的影子了, 这里在粘贴一些其定义:

所有左指针都是 δ-pointer.

从 ROOT 到任何叶子节点的每条路径都包含相同数量的 δ-pointer.

一些右指针可能是 σ-pointer, 但不存在连续的 σ-pointer.

在 二叉 B-树 中, 我们使用 δ-level 来表示其层级. 根据性质 2, δ-level 对于每一条到叶子节点的路径都是相同的. 这其实就是红黑树中最后一条性质: “对于每一个节点, 从该节点到期所有节点的简单路径上, 均包含相同数量的黑色节点”.

而被 δ-pointer 指向的节点就是 RED 节点, 否则为 BLACK 节点. 这就对应了红黑树中的性质一; 而 ROOT 节点必定不会被 δ-pointer 指向, 因此满足红黑树性质 2, 即 ROOT 一定为黑色节点.

而不存在连续 σ-pointer 便是红黑树中的性质 4, 即一个红色节点的两个子节点都是黑色的.

最后, 我们将所有最低 δ-level 上的所有被 σ-pointer 连接的叶子节点都赋予一个 BLACK 的 NIL 节点, 即可满足红黑树性质 3.

下面用一个手绘图展示一下等价过程:

// Binary B-Tree
//
      6 <ROOT> --------> 13
     /                /      \
    /              /            \
  /              /                  \
 2 --> 4        8 -----> 11          15
/    /   \     /    /         \    /     \
1    3    5    7    9 -> 10   12   14    16

// Binary B-Tree (With RED/BLACK Color)
//
       6(B) <ROOT> ------------------> 13(R)
      /                            /            \
     /                        /                      \
    /                    /                                \
 2(B) ---> 4(R)          8(B) ------> 11(R)                15(B)
  /        /   \          /      /             \           /     \
1(B)    3(B)    5(B)    7(B)    9(B) -> 10(R)   12(B)   14(B)    16(B)

// Red-Black Tree
//
                 6(B)
            /             \
      2(B)                  13(R)
      /   \             /          \
  1(B)   4(R)        8(B)          15(B)
          /   \      /  \           /   \
      3(B)  5(B)  7(B)   11(R)    14(B)  16(B)
                        /
                      9(B)
                        \
                         10(R)

不过 二叉 B-树 不够平衡, 主要是 σ-pointer 只能作为向右的横向指针, 树更倾向于 “向右倾斜”. 下面的 对称二叉 B-树 便用来解决这个问题.

对称二叉 B-树 (Symmetric Binary B-tree)

二叉 b-树 试图通过将 B-Tree 中固定大小的节点使用指针的方式进行空间上的优化以适应单极存储, 但存在缺点:

结构 “不够平衡”;
因为不够平衡导致其操作无法像平衡树一样保证在 O(lgh) (h 为树的高度);

In [3] binary B-trees were considered as a special case and a subsequent modification of the B-trees of [2]. Binary B-trees are derived in a straightforward way from B-trees they do exhibit, however, a surprising Asymmetry : the left arcs in a binary B-tree must be δ-arcs (downward), whereas the right arcs can be either δ-arcs or σ-arcs (horizontal). Removing this somewhat artificial distinction between left and right arcs naturally leads to the symmetric binary B-trees described here.

对称二叉 B-树与 二叉 B-树 一样, 也存在”水平 (horizontal)” (σ-pointer) 与 “垂直 (vertical)” (δ-pointer) 两种指针. 树在纵向的高度称之为 δ-level, 则有如下定义:

所有叶子节点都在同一 δ-level;
除 δ-level 最低一层的节点 (叶子节点) 外, 所有节点都有两个子节点.
不存在连续的 σ-pointer. (e.g. x1 -> x2 [-> x3] (INVALID))

下面是一个典型的树结构:

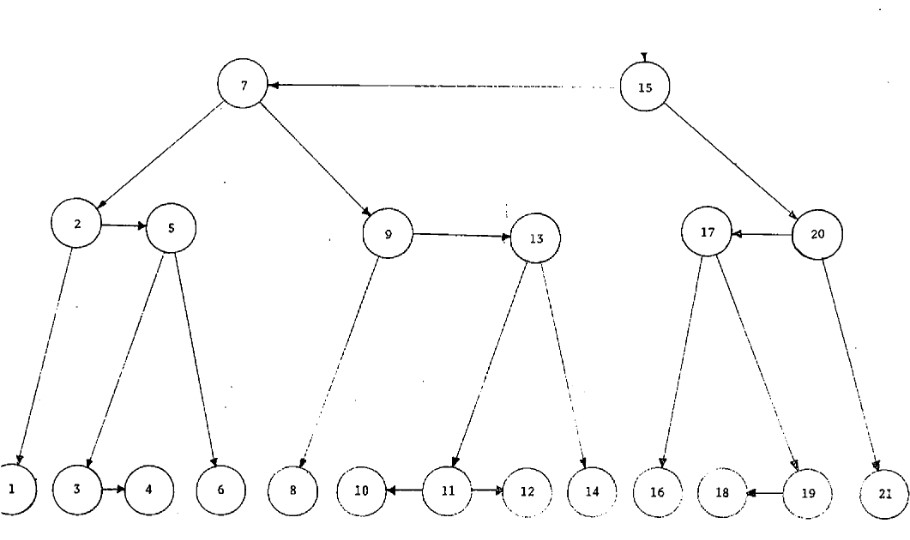
Symmetric Binary B-tree

δ-level
=======
 1                  7 <---------------------------------- 15 <ROOT>
               /         \                                  \
              /           \                                  \
             /             \                                  \
 2          2 -> 5           9 -------> 13              17 <- 20
           /    / \          /        /    \          /     \   \
          /    /   \        /        /      \        /       \   \
         /    /     \      /        /        \      /         \   \
 3      1    3 -> 4  6    8   10 <- 11 -> 12  14   16   18 <- 19   21

树高度: lg(N+1) <= h <= 2lg(N+2)-2, N 为节点数量, 证明见论文 SYMMETRIC BINARY B-TREES 中 “Number of Nodes and Height of a B-tree” 部分.

在上一节 (二叉 b-树)中, 我们将其与一个 k=1 的 B-Tree 进行等价, 这其实就是 2-3 树. 对称二叉 B-树 虽然允许 σ-pointer 向左右两边扩展, 但由于 性质2 约束 (除 δ-level 最低一层的节点 (叶子节点) 外, 所有节点都有两个子节点), 因此我们继续将其与 k=1 的 B-Tree 进行等价, 即 2-3 树.

// 同时加入 Red-Black Tree 对应的比较
//
//                      Symmetric
//                      Binary B-tree    B-tree (2-3 Tree)      Red-Black tree

// 2-Node                   x                                       x(R/B)
//                         / \              [p1 x p2]               /   \
//                        p1  p2                                  p1(B) p2(B)

// 3-Node(1)             x -> y                                    x(R/B)
//                      /    / \          [p1 x p2 y p3]           /   \
//                     p1   p2 p3                                p1(B)  y(R)
//                                                                     /  \
//                                                                  p2(B) p3(B)
//
// 3-Node(2)             x <- y                                    y(R/B)
//                      / \    \          [p1 x p2 y p3]           /   \
//                     p1 p2    p3                               x(R)  p3(B)
//                                                               /  \
//                                                             p1(B) p2(B)

下面概述插入和删除操作.

对称二叉 B-树插入 (Intert)

与二叉 B-树的插入类似, 我们找到需要插入的叶子节点, 并插入其 σ-pointer 中. 此时分为以下情况 (插入节点 z):

// case 1               1.1                  1.2
  |                       |                    |
  x              -->      x -> z          z <- x

// case 2               2.1                  2.2                2.3
                        (SPLIT_RR)            (SPLIT_RL)
  |                       |                    |               |
  x -> y         -->      x -> y -> z          x -> y     z <- x -> y
                                                z <-

// case 3               3.1                  3.2                3.3
                        (SPLIT_LL)            (SPLIT_LR)
       |                            |               |           |
  y -> x         -->      z <- y <- x          y <- x     z <- x -> y
                                                -> z

对于 case 1.1, 1.2, 2.3, 3.3, 已经完成插入, 流程结束.

而对于 case 2.1, 2.2, 我们需要进行一些变换修复性质, case 3.1, 3.2 是其镜像:

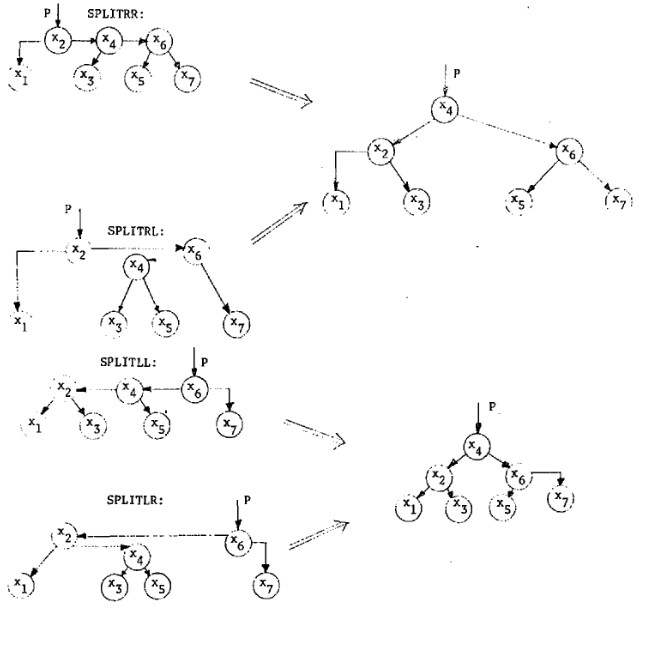
Insertion Algorithm

需要注意的是, 上图中原本 P 是一个 δ-arcs (由左或右 δ-pointer 指向), 修复后 P 变为一个 σ-arcs (由左或右 σ-pointer 指向).

    p
    |                               p --| <σ-arcs>
    x2 -> x4 -> x6      -->            x4
   *     /    /   \                 /     \
x1      x3   x5   x7              x2        x6
                                *   \      /  \
                              x1    x3    x5   x7

        p                             p
        |                             |
        x2 (B)                        x4 (R)
       /  \                         /    \
     x1    x4 (R)      -->       x2 (B)   x6 (B)
          /  \                   *  \     /  \
        x3   x6 (R)           x1     x3  x5   x7
            /  \
          x5    x7

    p
    |                               p --| <σ-arcs>
    x2 -------> x6      -->            x4
   *       x4 <-- \                 /     \
x1        /   \   x7              x2        x6
        x3    x5                *   \      /  \
                              x1    x3    x5   x7

        p                             p
        |                             |
        x2 (B)                        x4 (R)
       /  \                         /    \
     x1    x6 (R)      -->       x2 (B)   x6 (B)
          /     \                *  \     /  \
        x4 (R)   x7            x1     x3  x5   x7
       /  \
      x3

这样我们便将问题向上一层进行了转移 (原本 x2/x6 层的问题转变到了 P 所在层), 进行递归修复直到满足性质或者到达 ROOT 节点, 此时生成新的 ROOT 节点 x4.

对称二叉 B-树删除 (Deletion)

由于左右两侧能存在 σ-arcs, 删除相较二叉 B-树的删除更加复杂.

首先和前面一样, 先找到需要删除的节点 d 并视情况直接或者找到后继结点并交换后替换为 Dummy 节点.

后需也和前面一样, 可能存在性质破坏, 因此需要 (递归的) 修复性质, 具体如下:

// 原文中的图片看不清了, 手绘一个, 其中 * 表示可以是 σ-arcs 或者 δ-arcs.

// case a1: 在最低 `δ-level` 中
      p        p                    p
      |        |            =>      |      (DONE)
 z <- d  or    d -> z               z

// case a2: 在最低 `δ-level` 中, d 已经是叶子节点, 此时删除会导致违反性质1.
//          需要使用后面的 case b/c 进行修复.
      p
      |
      d    or    d <- p    or    p -> d

// case b 都是 d 位于父节点右侧 `δ-pointer` 的子节点, 分为以下四种情况

//   case b1: d 的兄弟节点 x2 位于父节点上, 但没有多余节点,
//            此时使用 MERGE 将问题向上推一层.
        p                         p
        *                         *
        x4                        d
      /     \                     |
     x2      d      =>      x2 <- x4     =>   .... (RECURSIVE)
   /    \    |            /   \     \
 x1     x3   x5          x1   x3    x5

//   case b2: d 的兄弟节点 x2 位于父节点上, 且右多余的节点, 兄弟节点性如下(case1).
//            此时执行 MERGE, 然后进行一次 SPLIT_LR 后, 回到 case a1 删除 d 即可.
          p                              p
          *                              *
          x4                             d
      /        \                         |
     x2 -> x3   d     =>         x2 <--- x4     => 执行一次 SPLIT_LR => (DONE)
    *           |               *  -> x3   \
  x1            x5             x1           x5

//   case b3: d 的兄弟节点 x2 位于父节点上, 且右多余的节点, 兄弟节点性如下(case2).
//            此时同样执行 MERGE, 然后进行一次 SPLIT_LL 后, 回到 case a1 删除 d 即可.
          p                               p
          *                               *
          x4                              d
       /      \                           |
x1 <- x2       d     =>       x1 <- x2 <- x4    => 执行一次 SPLIT_LL => (DONE)
       \       |                     \      \
        x3    x5                      x3     x5

//   case b4: d 的兄弟节点 x2 位于父节点左侧 σ-pointer 指向节点的右子树上.
              此时需要执行一下变化, 将 x2 提到上一层, 此时 为了保证 δ-level 不变,
              需要将 x3 作为 x4 左侧 σ-arcs 进行连接.
              此时会根据 x3 的形态产生三种不同的处理方式, 具体看下面说明,
              处理完成后即可结束算法 (所有性质都保持).
            p                   p
            *                   *
      x2 <- x4                 x2
     /  \   |                /    \
   x1   x3  d        =>    x1      x4            => (看下面说面)     => (DONE)
            |                  x3<-  \
            x5                         x5

//   => 此时 x3/x4 的关系可能是 case b2/b3 中第二步的一种或者 x3 没有 σ-arcs,
//      如果是 case b2/b3, 则执行对应的 SPLIT_LR 或者 SPLIT_LL 后, 算法结束.
//      如果 x3 没有 σ-arcs, 则什么也不用做, 直接结束算法即可.

// case c: d 是 x1 右侧 σ-arcs 对应的 节点, 此时直接将 x3 作为 x1 的右子树即可.
    p                     p
    |                     |
   x1 -> d      =>        x1        => (DONE)
         |                  \
         x2                   x3

// p 在左侧的情况与上述 case 完全镜像, 这里就不单独列出了.

需要注意的是, 如果 d 一直执行 case b1 移动到了 ROOT, 则 d 的后继结点 x4 便是新的 ROOT.

对称二叉 B-树小结

对称二叉 B-树 相对 二叉 B-树 主要是在平衡上进行修改, 从两者的插入流程就能一窥一二.

同时我们也将红黑树的概念与性质与之做一些对应:

	红黑树	对称二叉 B-树
	红色节点 (RED)	被 “水平 (horizontal)” (`σ-pointer`) 指针指向的节点
	黑色节点 (BLACK)	没有被 `σ-pointer` 指针指向的节点
	黑高 (Black-Height)	层数 `δ-level`
性质 1	一个节点只能是红色 (RED) 或者 (BLACK) 的	一个节点只能被 “水平 (horizontal)” (`σ-pointer`) 与 “垂直 (vertical)” (`δ-pointer`) 两种指针中的一种指向
性质 2	根节点是黑色 (BLACK) 的	根节点肯定不可能是被 `σ-pointer` 指向的
性质 3	每个叶子节点 (NIL) 是黑色 (BLACK) 的	所有叶子节点都在同一 `δ-level` (不需要红黑树中的 NIL 节点填充, 已经足够表达算法性质)
性质 4	如果一个节点是红的 (RED), 那么其两个子节点都是黑的 (BLACK)	不存在连续被 `σ-pointer` 指向的节点链. (e.g. `x1 -> x2 [-> x3] (INVALID)`)
性质 5	对于每个节点, 该节点到后代叶节点的简单路径上, 均包含相同数量的黑色 (BLACK) 节点	所有叶子节点都在同一 `δ-level` (这代表对于每个节点, 该节点到后代叶节点的简单路径上, 均包含相同数量的 `δ-arcs`)

也就是说, 我们可以通过:

将 σ-pointer 指向的节点染成红色 (RED), 其他节点染成黑色 (BLACK) (就是将 “边” 的改变转化为 “颜色”);
将 “边” 都替换为 “子树”;
将所有叶子结点都添加一个黑色的 NIL 节点.

便能将一个 对称二叉 B-树 转化为一颗 红黑树, 反之亦然.

总结

上面小节主要介绍了 二叉 B-树 与 对称二叉 B-树, 这些结构从 B-Tree 推导出来, 试图创建一种平衡树结构. 他们还不是二叉搜索树, 不过初版红黑树 (Red-Black Tree) 却是从这几种数据结构的基础上推导而来. 红黑树经过几十年的发展已经经过了很多版本的优化, 后面有时间的话我会从初版红黑树开始梳理红黑树的发展历程, 也希望能够帮助自己能够彻底理解这个数据结构.

参考资料

Twitter Facebook LinkedIn

Fries_I23